昨日、Python文法詳解を詳解する会 #3に参加してきました。第三回の主な内容は文字列と集合(set)だったんですが、 set ってよく知らないと何それおいしいの?状態だったりします。というか、自分も以前はそんな感じでした。
Python には配列として list があって、大抵のことはこれで事が済んでしまいます。list なら順番は保持してくれるし同じ値も格納することができます。それに対して set では順番が保持されないし同じ値を格納することもできません。一見するとすごく不便です。
set は、 l = list(set(l)) のように重複する要素を無くした list にするためにしか使わないという人は多いのではないでしょうか。
でも、実は set ってものすごく使える子なんですね。
set の何が嬉しいかっていうのを説明するには集合っていうものが何なのか?っていうことを説明したほうがいいんですが、細かい話をしだすとキリがないので気になる人は集合っていうキーワードで調べてみてください(丸投げ。
ここではあんまり詳しくなくても今日から使える set の使い方ということで、実例をあげて紹介します。
連番ファイルの抜けチェック
何かスクリプトを組む時に、あるデータ A と 別のデータ B が同じか、違うならどこが違うか?を比較したい時がよくあります。
映像業界では動画を扱う必要があるので画像を連番ファイルとして扱うことが日常的にあります。この時、一部のファイルが無くなってしまっているということが多々あります。
ファイルが 10 個とか 20 個とか少なければ目でも確認できますが、動画の連番ファイルは一秒で 24 個とか 30 個のファイルができます。10 秒で 240~300、一分なら 1440 とか 1800 個のファイルが一つのディレクトリ内にできます。ファイルの抜けがあるかどうかは総ファイル数を確認すればできます(後述の通り、本当はできないですが)。問題は、ファイルが少なかったり多かったりしたときです。
1440 個ファイルがなければいけないのに、1438 個しかファイルがなかった場合、どのファイルが無いのか確認しなければいけません。目視で確認?できなくはないですけど時間もかかるし見落としてしまったら再度チェックの必要があります。もっと悪いことに、正しいファイルは 1437 個で、本当はあってはいけないファイルが 1 個紛れ込んでいるかもしれません。こうなったらもう手あげです。こういうときはプログラムの出番です。
簡単に書くとこんな感じでしょうか。
import os
d = 'path/to/renban'
fname = 'hoge.%04d.exr'
nfile = 1000
for i in range(nfile):
path = os.path.join(d, fname % i)
if not os.path.exists(path):
print 'missing file :', path
はい。これで一応抜けているファイルのチェックはできるようになりました。でも、これだと余分なファイルがあった時にきづけないです。細かいことをしようとすると os.listdir() でファイル一覧を取得して、えいやっといろんな処理を書かないといけないです。めんどくさいです。めんどくさすぎて禿げてしまいます。
そういうときに、集合の比較という問題に落とし込んでしまいます。
連番ファイルのチェックという問題は、結局のところ
- 実際に存在するファイルの一覧
- 本来存在すべきファイルの一覧
の二つを比較するということです。一覧を集合と読み替えると、まさに集合演算の最も得意とする処理内容になります。そこで、コードにしてみましょう。まずはそれぞれの一覧(集合)を作ります。
import os
d = 'path/to/renban'
fname = 'hoge.%04d.exr'
nfile = 1000
# 実際に存在するファイルの一覧
existingFiles = set(os.listdir(d))
# 本来存在すべきファイルの一覧
theoreticalFiles = set([fname % i for i in range(nfile)])
これで集合ができました。あとは、この二つを好きなように集合演算すればいいだけです。
#本来あるべきなのに無いファイルを表示
print theoreticalFiles - existingFiles
#存在すべきでないファイルを表示
print existingFiles - theoreticalFiles
どうでしょう。引き算をするだけで欲しい情報が得られてしまいました。プログラムで逐次処理する例と比べて段違いに簡単で、かつ処理内容をちょっと変えるだけでいろいろな情報を得ることができるようになっています。
集合演算
ここで何をやっているのかを簡単に説明します。
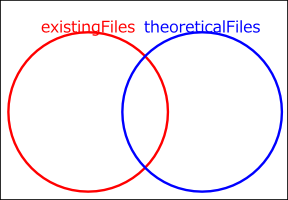
最初に作成した existingFiles と theoreticalFiles は下図のような関係にあります。赤い丸が existingFiles、青い丸が theoreticalFiles です。赤丸と青丸が重なっている部分は両方に含まれるファイル、重なっていない部分はどちらか片方にしか含まれないファイルになります。
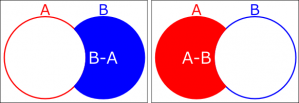
集合演算では、この丸を使って足したり引いたりといった演算を行うことができます。今回おこなったのは下図の二つの演算です(existingFiles と theoreticalFiles だと長いので、A と B に置き換えています)。みての通り、それぞれにしか含まれない要素だけを取り出すことができています。
もちろん、これだけではなく他にもいろいろな演算をおこなうことができるので、目的に応じて必要な情報を得ることができます。
まとめ
今回のような内容は、集合論の勉強をしたことのある人なら当たり前だよっていう内容ですが、知っていると知らないとでやりたいことを実現するためのアプローチが全く異なってくるといういい例です。
もちろん、集合(set) を使った処理をおこなうためには集合を扱うためのお約束に則った形に問題を置き換えなければいけないですが、うまく問題を置き換えることができた時には強力な道具になってくれます。
皆さんも身の回りの問題を置き換えて簡単に表現できないか考えてみてください。